-
- Evrenin Kozmik Modelleri
Evrenin geometrik formlarının incelenmesi topolojiye dayanmaktadır. Temelde sağda gösterilen Moebius filmi ile herkesin bildiği bu egzotik matematik alanı, örneğin yay ve yay içeren bir bardağın aynı topolojiye sahip olduğunu söylüyor: her ikisinde de hacimlerinde bir delik var, yolu değiştiren alan hangi unsurların birbirine bağlı olduğu, örneğin bir alanda bulunmayan deformasyonlar.
Hiper-boyuttaki bu delik, 1 olan Euler sayısına tekabül eder. Evrenimizle daha tutarlı olan deliksiz bir topolojik uzay durumunda, Euler = 0.
Topoloji yalnızca bağlantılarla ilgilenir ve nesnelerin büyüklüğü, şekli veya eğriliği ile ilgilenmez (pratikte örneğin yerçekiminin etkisi).
Topoloji, özellikle mekanla olanları ve mekan-zaman alanlarının birbirine bağlı olup olmadığını açıklayabilir. Kuantum kozmolojisini tartışırken bu olasılıkları tartışacağız.
Hepsinden önemlisi, Fransa Koleji’nde fahri profesör olan Jean-Clau de Pecker bize üç boyutlu evrenin (x, y, z) ve uzay-zamanın (x, y, z, t) geometrisini karıştırmamamızı hatırlatıyor.
Topolojide, boşluğun eğriliği, yüzeyinde tasarlanan iki ana bölümün eğrilik yarıçapının tersinin üretimine eşit olduğu tanımlanır. Eğer böyle bir küre enine kesilirse, aynı eğriliğe sahip iki yay vardır. Eğrilik pozitif olarak adlandırılır. Eksenine çapraz bir yüzey kesersek, iki dairesel yay zıt yönlerde eğrilere sahiptir. Eğrilik negatif olarak adlandırılır.
Bu nedenle, eğrilik doğrudan yüzeyde ölçülür ve koordinatların seçimine bağlı değildir. Metrik tarafından belirlendiğini söylüyorlar.

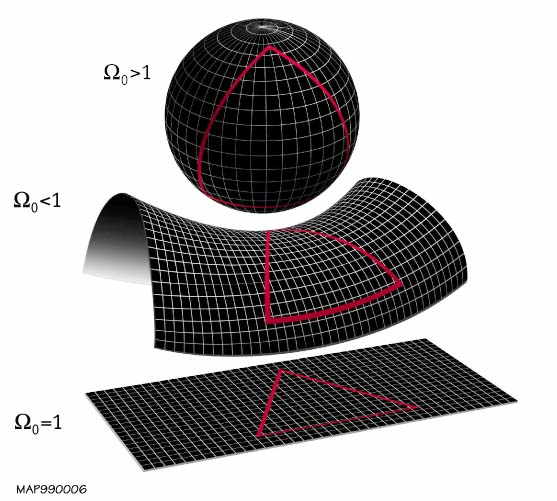
Evrenin Topolojisi Friedmann, topolojiyi inceleyerek, boş bir evren alanının daha önce söylediğimiz gibi bir düzlem olmadığını, ancak malzeme infüzyonu ona pozitif bir eğrilik verirken negatif bir eğrilik olduğunu keşfetti. Friedmann şu modeli keşfetti:
- Öklid, üç boyutlu model, hiçbir zaman bir arada bulunmayan paralel çizgiler olan klasik geometri yasalarına saygı gösteren tüm mekan biçimlerine uygulanır. Bir dairenin alanı (d cc) 42, hacmi 4 / 3πr3’tür. Bildiğimiz kadarıyla evren sonsuz iki boyutlu bir yüzeyle temsil edilebilir. Teoride, Öklid modeli, sonsuzluğa uzanan 10 sonsuz değişken ve 8 sonlu, silindirik boşluk ve rus içerir.
- Küresel model, sembolik olarak Öklid geometrisinin eksenlerinin artık uygulanmadığı bir küre ile temsil edilir. Boşluk eğridir ve üzerine kapanır. Eğrilik yarıçapı ile belirlenen bir mesafede birleşen iki paralel çizgi, bir dairenin alanı π2’den az, hacmi 4 / 3πr3’ten az. Bu geometrik model, sınırsız sayıda sonsuz sonlu alan biçimi içerir. Bu modelde, evrenimiz sınırsız olarak sınırlandırılabilir.
- Öklid geometrisi yasaları veya Öklidcilik kanunları için geçerli olmayan aşırı model (merkezsiz bir eyer ile temsil edilir). Ne anlama geldiğini anlayın: mesafe pozitif bir eğrilik yüzeyine ikiye katlandığında, toplam yüzey yarıçapın karesinin altında kalır ve bunun tersi aşırı negatif bir yüzeyde olabilir! Bir kürenin yüzeyinin düz bir yüzeye ve negatif bir yüzeyin kıvrılmalarının olmasının nedeni budur. Aşırı bir yüzey döngüsünün alanı π2’den yüksek olur ve hacmi 4 / 3πr3’ten büyüktür. Evren sonsuzdur. Açık veya kapalı olsun, aşırı model ayrıca sonsuz sayıda varyasyon içerir.
Biraz daha tanımlayacağımız gibi, Evrenin üç modelinde, uzayın eğriliği yarıçapı, R zamanla değişmektedir. Bu iki değişikliğe yol açar: büyürse evren genişler, azalırsa katkıda bulunur.
Evrenin Sonu. Ancak bu kavramlar belirsizdir. Şişirilmiş balonun ünlü imajını düşünerek aşırı veya küresel üç boyutlu bir evren sürekli olarak genişleyebilir. Ancak dört boyutta, aynı dünya zaman içindeki yarıçaptaki değişime göre istediğini yapabilir! … 3 boyutlu alanın şekli malzemenin dağılımına bağlıdır. Mekansal ve zamansal terbiye arasındaki bu belirsizlik göz önüne alındığında, çoğu astronom durdu ve bu kavramları kullanmamayı tercih etti.
Uygulamada, bir alanın alanını veya hacmini belirleyebilirsek, evrenin düz, açık veya kapalı (Euclid, aşırı veya küresel) olup olmadığını belirleyebiliriz. Bununla birlikte, bu tez elbette kanıtlanmamıştır, çünkü milyonlarca alanı, hatta milyarlarca ışıkyılı yılını ölçmek imkansızdır. İçerdiği madde miktarıyla yoğunluğunu, hacmini belirleyebilir ve evrimini öngörebiliriz. Bu kararlılığın birçok sorunu var ve bazen paradokslara yol açıyor. Sadece yeni matematik ve fiziki işlerin iskeleleri bu ikilemi çözer.